顯示廣告
隱藏 ✕
回列表(←)
Disp BBS guest 註冊 登入(i)
首頁(home) 上頁(↑) 下頁(↓) 末頁(end)
※ 本文轉寄自 ptt.cc 更新時間: 2025-07-22 20:33:42
看板 C_Chat
作者 Senkanseiki (戦艦棲姫)
標題 [閒聊] 老遊戲的變態程式碼
時間 Tue Jul 22 16:45:40 2025

https://www.youtube.com/watch?v=n2Q1Sp7iew4
https://en.wikipedia.org/wiki/Fast_inverse_square_root
Fast inverse square root - Wikipedia
[圖]
[圖]
[圖]
William Kahan and K.C. Ng at Berkeley wrote an unpublished paper in May 1986 describing how to calculate the square root using bit-fiddling techniques followed by Newton iterations.[4] In the late 1980s, Cleve Moler at Ardent Computer learned about this technique[5] and passed it along to his cowork ...

1999年製作的一款遊戲：Quake III Arena
在遊戲開發者之間，這款遊戲的程式碼成為了熱門話題
因為下面這個求1/√x的程式碼實在太變態了而讓大家頗為驚訝

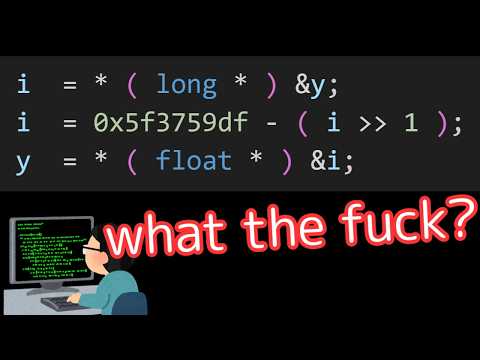
float Q_rsqrt( float number )
{
        long i;
        float x2, y;
        const float threehalfs = 1.5F;

        x2 = number * 0.5F;
        y  = number;
        i  = * ( long * ) &y;                       // evil floating point bit
level hacking
        i  = 0x5f3759df - ( i >> 1 );               // what the fuck?
        y  = * ( float * ) &i;
        y  = y * ( threehalfs - ( x2 * y * y ) );   // 1st iteration
//      y  = y * ( threehalfs - ( x2 * y * y ) );   // 2nd iteration, this can
be removed

        return y;
}

影片中有解說這個程式碼在幹什麼
簡單來說就是用好計算的加減乘除來取代複雜的求平方根的過程
因為現代電腦計算速度夠快，直接叫電腦求平方根也可以

但這款遊戲是1999年出的，求平方根這件事情是為了計算光影的強度
因為會影響到光影的計算速度，就算有一點誤差也希望可以大幅提速

畢竟就算有誤差，1%的明亮度差異應該大多數的人不會在意，所以速度比較重要


具體做了什麼可以參考影片內容
這個程式碼似乎是由某位數學教授想出來的
然後這個遊戲的製作人把數學教授的想法拿來活用的結果

各位有看過這種變態程式碼嗎？

--
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 61.64.25.104 (臺灣)
※ 作者: Senkanseiki 2025-07-22 16:45:40
※ 文章代碼(AID): #1eVq-scc (C_Chat)
※ 文章網址: https://www.ptt.cc/bbs/C_Chat/M.1753173942.A.9A6.html
→ gcobc12632: 雷神之鎚3算很有名的案例了吧1F 07/22 16:47
→ gcobc12632: 主要是0x5f3759df這個魔術數字是怎麼出現的
→ haoboo: 雷神之槌3的magic number3F 07/22 16:48
→ yamis: 聽說是牛頓法算出來的4F 07/22 16:49
→ npc776: 卡馬克自己都不記得怎麼寫出來的 什麼時候變成數學教授了5F 07/22 16:49
推 ninnyshadow: 文組看不懂 誰能解釋的白話一點QQ6F 07/22 16:49
→ npc776: 用一句話把一件事講了個大概準確 在容量只有一行時 很神7F 07/22 16:51
推 SPDY: 這很有名啊 看注釋在WTF 就在嘴能用卻不能理解原理8F 07/22 16:51
→ vios10009: 這種東西都稱為魔術數字，把計算合在一起的結果，對於9F 07/22 16:51
→ vios10009: 低效能的電腦很有用，但沒任何註解就沒人知道怎麼來的
→ ack0011: 以前都要考慮有限的效能能做多少事情，現在都直接靠硬體11F 07/22 16:53
→ ack0011: 效能直接車過去，跑不動的請自己換頂級硬體
→ haoboo: 性能有限的時候拿來快速跑出近似解而不是最佳解13F 07/22 16:53
→ lazioliz: 卡馬克最近在開發AI的樣子14F 07/22 16:54
推 neetarashi: // what the fuck?  我有時候也會寫出這種註解w15F 07/22 16:54
推 RockZelda: 好像用到找平方根的牛頓-拉森佛方法16F 07/22 16:55
推 abysszzz: 這個案例好像蠻有名的，幾年前就看過有人講17F 07/22 16:55
推 lovez04wj06: 註釋應該是接手的人寫的吧，不然真就窮舉法了= =18F 07/22 16:56
→ npc776: 20年來都有人在講 不過算了 現在不弄短影音就沒人看過似的19F 07/22 16:56
→ nineflower: 數學不好要怎麼寫程式？20F 07/22 16:59
推 SPDY: 粗略來說就計算光線之類需要平方根倒數 老實算很慢21F 07/22 17:00
→ SPDY: 這個就減少計算浮點能用整數就好 快得多取得近似值
推 orze04: FIS啊 別問 用就是了23F 07/22 17:03
→ orze04: 這段的關鍵是WTF這段註解
推 SPDY: 那0x5f3759df也不是唯一能用 WiKi上有中文條目可看25F 07/22 17:05
推 meatybobby: 插值法吧 記得這個數字不是最佳解但也很接近了26F 07/22 17:12
推 tommy89082: 卡馬克也不是發明者，據說是從古早黑客論壇流出的27F 07/22 17:12
推 Aether13: 以前是用數學來幫助程式 例如1 + 到100 可以用for迴圈慢28F 07/22 17:16
→ Aether13: 慢sum 但用梯形公式更快 現在就是反過來用大量運算來模
→ Aether13: 擬某個行為後再分析結果 已經變成用程式來幫助數學了
推 wei115: 就是快速平方根倒數阿 那個常數比較神奇 數學論文只給出31F 07/22 17:17
→ wei115: 某個範圍的數當初值比較好 這個常數是最好的值
→ wei115: 有人就推測作者是直接窮舉 用程式跑完那個範圍的數 找出最
→ wei115: 好的那個值
→ qd6590: 這老熟了35F 07/22 17:21
推 llabc1000: // what the fuck36F 07/22 17:40
推 Porops: https://youtu.be/g1r3iLejTw037F 07/22 17:40
→ Porops: 這個議題有人有做中文解說影片
推 ayaneru: 問就是wtf39F 07/22 17:41
推 orze04: 卡瑪克有說不是自己發明的，只知道是當時負責雷神之錘項40F 07/22 17:42
→ orze04: 目的一個碼農
推 Zchanya: 以前資結聽過介紹好像是用計算尺之類的去填表格 找出那個42F 07/22 17:42
→ Zchanya: 16制值
推 grtfor: 以前程式就是有很多創意的解，現在大概就直接問AI就完事44F 07/22 17:45
推 as920909: 最快的算法永遠是公式解 O(1)45F 07/22 17:47
→ PROMAC: 以前硬體性能不好激發各種創意46F 07/22 17:48
推 orze04: 比那個年代更早之前靠人力計算做出SR71和登月軌道47F 07/22 17:48
推 yeay: 老程式很常有這種magic number48F 07/22 17:53
推 supersusu: It just works49F 07/22 17:54
推 b325019: 很多影片都說明過這個數值50F 07/22 17:59
→ b325019: SR71最神奇的是他那顆引擎的
推 goisjkps: 遊戲偏前端 所以可以規劃遊戲的時候就先算好然後套數字52F 07/22 18:05
→ goisjkps: 進去來節省計算資源
推 kirimaru73: 那不是最佳解 只是誤差程度很變態54F 07/22 18:18
→ kirimaru73: 實際上用起來效率跟最佳解沒有多少差別 不用的話則是
→ kirimaru73: 爆慢
推 kirimaru73: 這種功能程式把數字寫死是合理的 當然要直接寫死
→ kirimaru73: 變態的是你為什麼知道那個數字
推 PetrVanis: 程式寫多一點都會遇到 大概是跑數值分析出來的值直接59F 07/22 18:27
→ PetrVanis: 套用
推 kor525: 太神啦61F 07/22 18:30
推 orze04: 最神奇是裡面沒有除法62F 07/22 18:31
推 devilhades: Old school電腦時代的藝術63F 07/22 18:33
→ deflife: 就牛頓法+浮點數表示法64F 07/22 18:42
→ JamesChen: 不就近似嗎，很直觀就會想到的啊65F 07/22 18:42
推 crazy6341556: 不是單純的近似 那個值怎麼找很有門道路66F 07/22 19:51
推 b325019: 這個快速算法的精髓就在於那個起始值的挑選67F 07/22 20:01

--
※ 看板: ACG　文章推薦值: 0 目前人氣: 4 累積人氣: 2675　
作者 Senkanseiki 的最新發文:
點此顯示更多發文記錄
分享網址: 複製 已複製
1樓 時間: 2025-07-22 23:19:09 (台灣) 
→
scottcheng
　    (編輯過) TW 
我以前讀過一本書, 跟數值計算有關, 裡面牽涉到 sin cos , 開根..等等的快速計算, 重點是用asm 寫的. 所以計算其實是用事先算好的數值做 asm 最簡單的 ++--.. 所以那個fuck數字大概就是類似方法做出來的..不過這只是我猜測. 這種 預先算好的方式, 其實最後誤差應該會蠻大. 早期不是每個人電腦都有 數學輔助處理器, 但後期都直接放到cpu裡面了. Quake III Arena 已經算後期了, 自己搞一個算法大概是老人才會幹的事
r)回覆 e)編輯 d)刪除 M)收藏 ^x)轉錄 同主題: =)首篇 [)上篇 ])下篇